Adaptive control of hybrid modes in a longitudinally magnetized gyroelectromagnetic circular waveguide
DOI:
https://doi.org/10.1109/ICATT.2017.7972653Keywords:
circular waveguide, effective medium theory, hybrid wavesAbstract
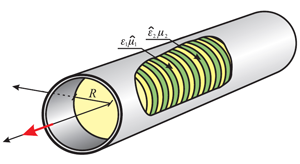
In this report, dispersion properties of a circular waveguide filled by a composite gyroelectromagnetic structure, which consists of alternating ferrite and semiconductor layers are studied. The system is supposed to be longitudinally magnetized, i.e. the static external magnetic field is applied along the axis of the guide, perpendicularly to the layers of the structure. The system is considered to be in the subwavelength regime, and the relative effective permittivity and permeability of the waveguide filling are introduced. The waveguide dispersion equation and its eigenmodes are derived. Unique dispersion characteristics of supported hybrid modes are investigated. It is shown that simultaneous presence of gyromagnetic and gyroelectric eifects in the waveguide system can gain a substantial control under the dispersion characteristics and field distributions of the supported modes.References
B. Ghosh, and A. B. Kakade, “Guided modes in a metamaterial-filled circular waveguide,” Electromagnetics, vol. 32, pp. 465-480, 2012. DOI: http://doi.org/10.1080/02726343.2012.726913.
T. Gric, L. Nickelson, and S. Asmontas, “Electrodynamical characteristic particularity of open metamaterial square and circular waveguides,” Prog. Electromagn. Res., vol. 109, pp. 361-379, 2010. DOI: http://doi.org/10.2528/PIER10082505.
V. R. Tuz, I.V. Fedorin, V. I. Fesenko, H.-B. Sun, V. M. Shulga, and W. Han, “Dispersion peculiarities of hybrid modes in a circular waveguide filled by a composite gyroelectromagnetic medium,” J. Electromagnet. Wave, vol. 31, pp. 350-362, 2017. DOI: http://doi.org/10.1080/09205071.2017.1285726.
Y. Yorozu, M. Hirano, K. Oka, and Y. Tagawa, “Modes in dielectric or ferrite gyrotropic slab and circular waveguides, longitudinally magnetized, with open and completely or partially filled wall,” J. Opt. Soc. Am. B, vol. 27, pp. 1965-1977, 2010. DOI: http://doi.org/10.1364/JOSAB.27.001965.
W. Che, E. K. Yung, J. Wen, “Cutoff characteristics of modes in a circular waveguide filled with microwave ferrite,” J. Electromagnet. Wave, vol. 16, pp. 1103-1118, 2002. DOI: http://doi.org/10.1163/156939302X00651.
I. Fedorin, “Polarization transformation by a hyperbolic metamaterial on a metal substrate,” Prog. Electromagn. Res. B, vol. 67, pp. 17-30, 2016. DOI: http://doi.org/10.2528/PIERB16011702.
V. R. Tuz, V. I. Fesenko, I. V. Fedorin, H.-B. Sun, and W. Han, “Coexistence of bulk and surface polaritons in a magnetic-semiconductor superlattice influenced by a transverse magnetic field,” J. Appl. Phys., vol. 121, p. 103102, 2017. DOI: http://doi.org/10.1063/1.4977956.
V. R. Tuz, V. I. Fesenko, I. V. Fedorin, H.-B. Sun, and V. M. Shulga, “Crossing and anti-crossing effects of polaritons in a magnetic-semiconductor superlattice influenced by an external magnetic field,” Superlattices Microst., vol. 103, pp. 285-294, 2017. DOI: http://doi.org/10.1016/j.spmi.2017.01.040.
V. I. Fesenko, I. V. Fedorin, and V. R. Tuz, “Dispersion regions overlapping for bulk and surface polaritons in a magnetic-semiconductor superlattice,” Opt. Lett., vol. 41, pp. 2093-2096, 2016. DOI: http://doi.org/10.1364/OL.41.002093.
V. R. Tuz, “Polaritons dispersion in a composite ferrite-semiconductor structure near gyrotropic-nihility state,” J. Magn. Magn. Mater., vol. 419, pp. 559-565, 2016. DOI: http://doi.org/10.1088/2040-8978/17/3/035611.
A. G. Gurevich, Ferrites at Microwave Frequencies. Heywood, London, 1963.